Профориентационное образовательное мероприятие "Горизонты Образования" в образовательных учреждениях города Иркутск.
Профориентационное образовательное мероприятие "Горизонты Образования" в образовательных учреждениях города Владивосток
Профориентационное образовательное мероприятие "Горизонты Образования" в образовательных учреждениях города Хабаровск
Профориентационное образовательное мероприятие "Горизонты Образования" в образовательных учреждениях города Саратов
Профориентационное образовательное мероприятие "Горизонты Образования" в образовательных учреждениях города Самара
Профориентационное образовательное мероприятие "Горизонты Образования" в образовательных учреждениях города Казань
Колледж электроники и приборостроения
Санкт-Петербургский горный университет, СПГУ
Справочник
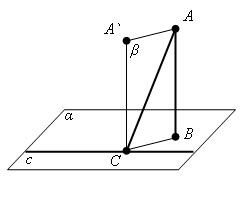
Теорема о трех перпендикулярах
|